Continuing the innovation and application of machine learning to the hardest and most impactful challenges, InstaDeep is pleased to share its new breakthrough on applying reinforcement learning to complex combinatorial problems. Our new work, “Population-Based Reinforcement Learning for Combinatorial Optimization” introduces a new framework for learning a diverse set of complementary agents, and obtains state-of-the-art reinforcement learning (RL) performance on three famous challenges: the travelling salesman, knapsack, and capacitated vehicle routing problems (TSP, KP, and CVRP).
Machine learning for combinatorial problems
From packing a delivery van with parcels and optimising its route, to designing a computer chip and scheduling the factory tasks to manufacture it, many of the hardest problems across a range of application domains share a common theme – they can be formulated as Combinatorial Optimization (CO) problems. Formally, a CO problem considers a discrete set of variables (e.g. items/locations); and the task is to find a labelling (e.g. placements/visitation order) that optimises some objective function (e.g. packing volume, route length). However, despite their ubiquitous nature, such problems are highly challenging (often NP-hard), with the number of possible solutions typically growing exponentially with the problem size.
This hasn’t stopped researchers from developing a vast array of heuristics for CO problems – algorithms that, whilst not guaranteeing an optimal solution, can often provide good performance in a reasonable timeframe. The downside is that this often requires extensive expert knowledge, human effort and ingenuity for each unique problem. An alternative approach is to apply machine learning techniques to automatically learn heuristics. In this vein, RL is particularly attractive as it removes the need for generating pre-solved instances for training and can readily represent CO problems using states, actions and rewards. For example, in TSP, which considers the shortest route visiting every city, the state can be expressed as the map and current route, the action as the next city to visit, and the reward as the negative distance travelled.
Populations of RL solvers
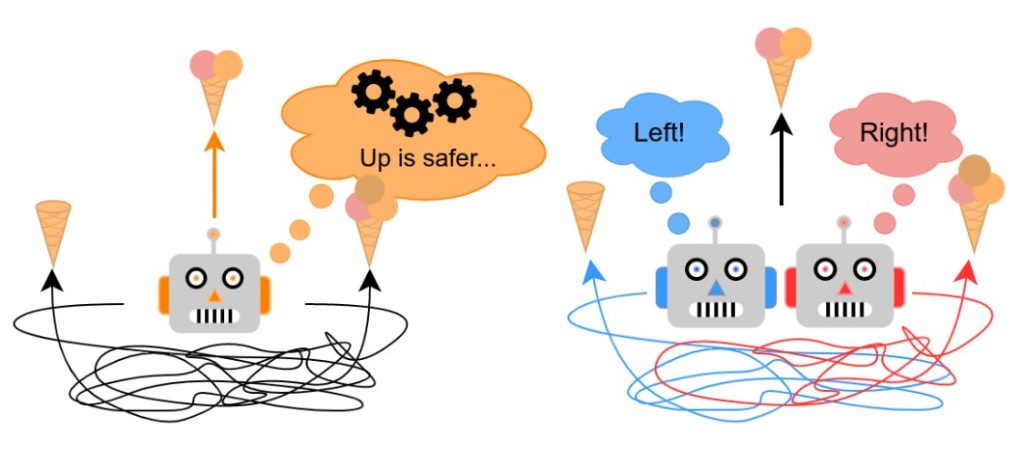
The project began by asking ourselves the fundamental question: “Why are CO problems so challenging for RL agents to solve?”. Let’s consider an (ice-cream loving) agent faced with three paths, two of which are a complicated maze which leads to either a three-scoop ice cream cone or an empty cone, and a third, safe path, that clearly leads to two scoops. If the agent cannot solve the maze reliably, it will eventually learn to choose the safe path, as this gives more ice-cream in expectation. Now, what would happen if we considered a two-agent population instead? Crucially, the population can trivially guarantee finding the three-scoop ice cream: the agents simply need to take opposite paths through the maze.
We argue that the ice cream problem is similarly descriptive of solving a CO problem: different paths through the maze can be viewed as the different sequences of actions an agent can take. However, if the problem is sufficiently complex, the agent will not initially know which path is optimal and thus, will ultimately learn to favour safer strategies rather than exploring riskier strategies that may or may not be optimal. Our key insight is that a population of agents with suitably diverse policies – where no agent is required to be good on all problems, but instead only one agent needs to be performant on any given problem – can better explore the solution space of hard CO problems and effectively trade-off this risk-reward dilemma.
Our method – Poppy
Converting the intuition above into a performant training strategy is not straightforward. Our proposed approach, dubbed Poppy, deals with the following challenges:
Challenge #1: Train diverse agents without explicitly specifying how they should differ from each other.
Solution: We introduce a new training objective that maximises population-level performance – that is to say each agent does not need to be performant for every possible problem, but rather only one agent needs to be good for any given problem. In practice, this is realised by training an agent only on the subset of training samples on which it is the best amongst the entire population. Crucially, this approach does not rely on specific notions of diversity and, hence, it is applicable to a wide range of problems.
Challenge #2: Keep the computational cost of training a population manageable. Intuitively, training more agents incurs a higher computational burden.
Solution: Poppy addresses this through parameter sharing and a multi-stage training process where the shared parameters are first optimised using a single agent, before per-agent parameters are specialised using the Poppy objective.
SOTA performance
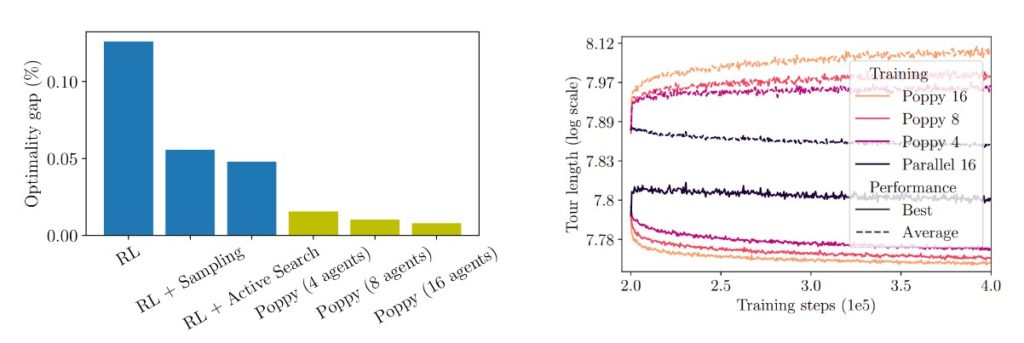
We evaluated Poppy on several CO problems and observed substantial improvements with respect to previous approaches in terms of the quality of the solutions and the time needed to produce these given a trained model. In the case of TSP, we found small populations to be enough to generate diverse solutions (top) and get state-of-the-art RL results (bottom left)! The performance-driven diversity is observed when a set of pre-trained agents are specialised with Poppy (bottom right): while the average performance of all agents in the population worsens, the performance of the population as a whole dramatically improves. Indeed, the effect is even stronger for larger population sizes since agents can learn increasingly specialised strategies. Ultimately, on TSP, Poppy outperforms the even state-of-the-art active-search approaches (where a single agent is fine-tuned on each problem instance); dividing the optimality gap by 5 while reducing the inference time by more than an order of magnitude.
We believe that population-based approaches offer a promising direction for many challenging problems and our hope is that innovations such as Poppy can broaden the range of potential applications. At InstaDeep, we are committed to continue pushing the boundaries of machine learning research and applications – if you would like to be a part of this journey, check out our opportunities at www.instadeep.com/careers.

