(Part 1/4)
The recent developments in Reinforcement Learning (RL) have shown the incredible capacity of computers to outperform human performance in many environments such as Atari Games [1], Go, chess, shogi [2], Starcraft II [3]. This performance results from the development of Deep Learning and Reinforcement Learning methods like Deep Q-Networks (DQN) [4] and actor-critic methods [5, 6, 7, 8]. However, one essential advantage of human intelligence on artificial agents is the capacity to understand and adapt quickly to new tasks using prior experience on similar tasks. This is what Meta-Reinforcement Learning (Meta-RL) is all about.
In this series of posts, you will understand how to design and train agents demonstrating human-level adaptability and the capacity to improve their performance with additional experience. You will also gain a general view of the problems Meta-RL can solve and understand the multiple existing algorithms.
A concrete Meta-RL problem
The goal of Meta-RL is to design agents that can adapt quickly and improve with additional experience. But concretely, what does it mean?
Let’s consider a classical control task like HalfCheetah, introduced by physics engine MuJoCo. In this environment, you control a 2D cheetah robot and the goal is to make it run forward as fast as possible.
Now, let’s consider a slight modification of the environment that includes a goal speed. The goal of the agent is to run forward and reach this speed. However, this goal is not observed and the agent has to infer it from the rewards received. Initially, the agent has no prior knowledge about movement, environment, and objective. It is simply an untrained neural network that observes a state vector and occasionally receives rewards. Given a goal speed v and using an actor-critic method with continuous control like PPO [6], we can teach the agent to run forward at speed v. However, imagine we now want to consider a new goal speed v’ ≠ v. How can we make our robot run at speed v’?
Of course, we could simply send our agent back into the environment and retrain it to adapt to the new goal. However, the learning process is unpredictable and we have no idea how quickly the agent can learn a new policy. But intuitively, the agent has acquired knowledge about dynamics, forward movement, and target speed. Given a good and informative signal from the environment, we would like the agent to adapt quickly and update its policy to reach the new target speed. Designing agents with such properties is the goal of meta-reinforcement learning!
The formal Set-Up of Meta-RL
First, let’s start by recapitulating the formalism of Reinforcement Learning to see how Meta-RL differs from it. In RL, we consider a Markov Decision Process (MDP) M = (S, A, γ, T, R) where S is the state space, A is the action space, γ is the discount factor, T is the transition distribution, R is the reward function. Given a set of parametrised policies, the goal is to optimise the objective:
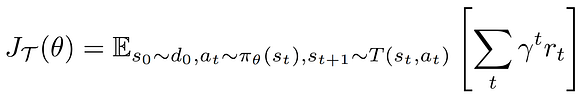
In Meta-RL, we are not given a single Markov Decision Process but a distribution of Markov Decision Processes with the same state space and action space but distinct transition distributions and reward functions. Each MDP is called a task and we consider a distribution over these tasks:

Note: In the general setting, we consider that the transition distributions and reward functions can be distinct across tasks. In practice, for most of the tasks, we will only consider the rewards to be distinct.
A few Meta-RL environments
Before moving to our meta-learning algorithms, let’s introduce a few examples of meta-learning environments. They will be a benchmark for the various methods we will introduce and will be used to evaluate the performance of the meta-reinforcement learning algorithms.
MuJoCo is a well-known standard benchmark for Reinforcement-Learning algorithms. Two main MuJoCo environments are the Ant and HalfCheetah, where the goal is to run forwards as quickly as possible. Let’s present two meta-environments derived from them introduced in [9]:
- Forward/Backward Ant and HalfCheetah. In these two environments, the goal is to run as quickly as possible, either forwards or backwards. There are two tasks.
- Random Ant and HalfCheetah. In these two environments, the goal is to run forwards and reach a random speed. This distribution of tasks is continuous, parametrised by speed v ∼ U([0, 2]) for the cheetah and v ∼ U([0, 3]) for the ant.
These two environments are considered the baseline tasks of Meta-RL. An algorithm that solves these tasks demonstrates strong adaptability skills.

In addition, we also consider three environments introduced in [10].
- Firstly, let’s consider Robotic Manipulation. In this environment, the tasks consist of fetching blocks and pushing them to a certain goal. The distribution of tasks is parametrised by the location of blocks and goals.

- We also consider the two locomotion tasks: wheeled locomotion and ant locomotion. For these environments, a robot has to navigate to different goals. The tasks are parametrised by the different goal locations. The wheeled robot controls its 2 wheels. The ant controls its 4 legs.

Contrary to Forward/Backward and Random Ant/HalfCheetah, the robotic manipulation and locomotion tasks have sparse rewards. This makes these environments much more challenging because the agent needs to explore before adapting its policy. An algorithm that solves these tasks demonstrates the capacity to conduct structured exploration.
- In addition to this 2D-navigation control environment, we introduce an equivalent discrete environment. The agent moves on a 2D grid and has to find a single goal. It always starts from a fixed start location and the distribution of tasks is parametrised by the unobserved goal location.

- Finally, let’s introduce the Maze2D/Maze3D environments introduced in [11] as well as an extension, 3D Visual Navigation, from [12]. In these environments, an agent is navigating in a 3D world and must find information to know the goal.
In addition to the sparsity of the rewards, another difficulty of both Maze2D and Maze3D is to decouple exploration from exploitation. Indeed, we first need to execute a policy to infer the task (navigate to the grey box) before exploiting the inferred task (navigate to the blue/red box). On top of these challenges, 3D Visual Navigation adds another difficulty: inferring the task from a visual signal.



Meta-training and meta-testing
Right, so we have this distribution of tasks, but what exactly do we want to do? One idea might be to find an optimal policy π* for this distribution of tasks, maximising the expected return. This is called multi-task learning: a single policy should maximise the expected return over tasks.

But what does this give in practice and can we solve this problem? For a more concrete understanding, let’s consider our HalfCheetah example. We consider a uniform distribution over target speeds v ∼ U([0, 3]). The transition distribution is the same for every task, and, given a task i with a target speed vᵢ, the reward function is Rᵢ(s) =−(v − vᵢ)². In this example, a multi-task algorithm would learn to converge to a speed v=1.5 maximising the average return. Not very satisfying, is it?
Realistically, we cannot learn a single policy for this multi-task setting. This leads us to the core elements of meta-learning: meta-training and meta-testing.
As we have seen, since a single policy cannot solve all tasks, we want to learn a good algorithm to quickly compute an optimal policy for the new task. There is a common structure to all meta-RL algorithms: they are divided into two distinct steps.
- In the first step, called meta-training, the goal is to learn an algorithm.
- In the second step, called meta-testing, we apply this algorithm to learn a good policy for the current task.

Conclusion
- Despite the great developments in RL, common methods don’t allow agents to understand and adapt quickly to new tasks using prior experience. In Meta-RL, we design agents to leverage prior experience on similar tasks.
- The formal set-up of Meta-RL slightly differs from traditional RL. Instead of considering a single MDP (Markov Decision Process), we consider a distribution of MDPs with the same state and action space. Examples of such tasks can be the HalfCheetah environment with a continuous distribution of goal speeds or the Ant 2D-Navigation with a distribution of goals on a semicircle.
- Meta-RL is divided into 2 steps: meta-training, where we learn an algorithm, and meta-testing, where we apply this algorithm to learn an optimal policy.
You can see the results at meta-test time from the DREAM algorithm where the agent learns to read a sign, recognise the colour and go to the matching key:
Do you want to learn how these Meta-RL algorithms work? Follow this series of blog posts:
 |  |
Do you want to learn how these Meta-RL algorithms work? Follow this series of blog posts:
- Firstly, you will learn about gradient methods for Meta-RL, such as MAML. They work extremely well and can solve almost any dense environment.
- You will then learn how to overcome the limits of MAML and solve sparse environments with MAESN and PEARL.
- Finally, we will introduce the most recent and advanced methods using recurrent and Bayesian methods.
References
[1] Adria Puigdomenech Badia, Bilal Piot, Steven Kapturowski, Pablo Sprechmann, Alex Vitvitskyi, Zhaohan Daniel Guo, and Charles Blundell. Agent57: Outperforming the atari human benchmark. CoRR, abs/2003.13350, 2020.
[2] Julian Schrittwieser, Ioannis Antonoglou, Thomas Hubert, Karen Simonyan, Laurent Sifre, Simon Schmitt, Arthur Guez, Edward Lockhart, Demis Hassabis, Thore Graepel, Timothy P. Lillicrap, and David Silver. Mastering atari, go, chess and shogi by planning with a learned model. CoRR, abs/1911.08265, 2019.
[3] Oriol Vinyals and Igor Babuschkin. Grandmaster level in starcraft ii using multi-agent reinforcement learning. 2019.
[4] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin A. Riedmiller. Playing atari with deep reinforcement learning. CoRR, abs/1312.5602, 2013.
[5] Volodymyr Mnih, Adri`a Puigdom`enech Badia, Mehdi Mirza, Alex Graves, Timothy P. Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu. Asynchronous methods for deep reinforcement learning. CoRR, abs/1602.01783, 2016.
[6] John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. Proximal policy optimization algorithms. CoRR, abs/1707.06347, 2017.
[7] Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. CoRR, abs/1801.01290, 2018.
[8] Lasse Espeholt, Hubert Soyer, R´emi Munos, Karen Simonyan, Volodymyr Mnih, Tom Ward, Yotam Doron, Vlad Firoiu, Tim Harley, Iain Dunning, Shane Legg, and Koray Kavukcuoglu. IMPALA: scalable distributed deep-rl with importance weighted actor-learner architectures. CoRR, abs/1802.01561, 2018.
[9] Chelsea Finn, Pieter Abbeel, and Sergey Levine. Model-agnostic metalearning for fast adaptation of deep networks. CoRR, abs/1703.03400, 2017.
10] Abhishek Gupta, Russell Mendonca, Yuxuan Liu, Pieter Abbeel, and Sergey Levine. Meta-reinforcement learning of structured exploration strategies. CoRR, abs/1802.07245, 2018.
[11] Pierre-Alexandre Kamienny, Matteo Pirotta, Alessandro Lazaric, Thibault Lavril, Nicolas Usunier, and Ludovic Denoyer. Learning adaptive exploration strategies in dynamic environments through informed policy regularization. CoRR, abs/2005.02934, 2020.
[12] Emanuel Todorov, Tom Erez, and Yuval Tassa. Mujoco: A physics engine for model-based control. In 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, pages 5026–5033, 2012.
[13] Yan Duan, John Schulman, Xi Chen, Peter L. Bartlett, Ilya Sutskever, and Pieter Abbeel. Rl2: Fast reinforcement learning via slow reinforcement learning, 2016.
[14] Erin Grant, Chelsea Finn, Sergey Levine, Trevor Darrell, and Thomas L. Griffiths. Recasting gradient-based meta-learning as hierarchical bayes. CoRR, abs/1801.08930, 2018.
[15] Alex Nichol, Joshua Achiam, and John Schulman. On first-order metalearning algorithms. CoRR, abs/1803.02999, 2018.
[16] Luisa M. Zintgraf, Kyriacos Shiarlis, Vitaly Kurin, Katja Hofmann, and Shimon Whiteson. CAML: fast context adaptation via meta-learning. CoRR, abs/1810.03642, 2018.
[17] Kate Rakelly, Aurick Zhou, Deirdre Quillen, Chelsea Finn, and Sergey Levine. Efficient off-policy meta-reinforcement learning via probabilistic context variables. CoRR, abs/1903.08254, 2019.
[18] Jan Humplik, Alexandre Galashov, Leonard Hasenclever, Pedro A. Ortega, Yee Whye Teh, and Nicolas Heess. Meta reinforcement learning as task inference. CoRR, abs/1905.06424, 2019.
[19] Luisa M. Zintgraf, Kyriacos Shiarlis, Maximilian Igl, Sebastian Schulze, Yarin Gal, Katja Hofmann, and Shimon Whiteson. Varibad: A very good method for bayes-adaptive deep RL via meta-learning. CoRR, abs/1910.08348, 2019.
[20] Evan Zheran Liu, Aditi Raghunathan, Percy Liang, and Chelsea Finn. Explore then execute: Adapting without rewards via factorized meta reinforcement learning. CoRR, abs/2008.02790, 2020.
Thanks to Alex Ltr, Clément Bonnet, and Paul Caron.



