
Learning a wide variety of skills that can be reused to learn more complex skills or solve new problems, is one of the central challenges of AI. In this research project in collaboration with Scott Reed and Nando de Freitas, we worked on answering the following question: How can knowledge acquired in one setting be transferred to other settings? A powerful way to achieve this goal is through modularity. Imagine you want to teach a robot how to cook your favourite meal. First, you have to teach it how to chop vegetables, how to fry them, etc. Secondly, to chop vegetables, the robot must learn how to use a knife, how to use a chopping board, how to properly clean your vegetables, and so on. This paper aims to exploit modularity to learn to solve complex problems with neural networks by decomposing them into simpler ones to be solved first.
Learning Neural Programs
We want to create libraries of programs that can be re-used to compose and implement more complex ones. Why learning programs? Because they are very versatile and appear in many forms in AI; for example as image transformations, as structured control policies, as classical algorithms, and as symbolic relations. We focus on a particular modular representation known as Neural Programmer-Interpreters (NPI). In their original work, Scott Reed and Nando de Freitas showed how to teach libraries of programs neural networks to achieve impressive multi-tasking results, with strong improvements in its generalisation capacities and reductions in sample complexity. Notably, they trained their architecture to sort lists of 20 digits with the Bubble sort algorithm. Once trained, the network was able to transfer the skills acquired to sort lists consisting of up to 60 digits.
The results proved NPI was able to learn complex hierarchical libraries of programs. Before learning the Bubble sort, it was taught simpler programs such as conditionally swapping elements or moving pointers at the beginning of the list. Once all these low-level programs were mastered, it learned how to combine them to implement the full Bubble sort algorithm. NPI was also shown to be able to learn recursive programs. such as the recursive version of the Bubble sort algorithm.
In its original setting, NPI was trained using supervised learning on programs execution traces which requires the knowledge of program implementation. While this provides strong evidence of the NPI architecture power, this approach has limitations. This research proposes to replace the setting of supervised learning by reinforcement learning. We alleviate the need for execution traces by execution tests on the programs we want to learn. In other words, this approach allows us to train an agent by telling it what to do, instead of how to do it.
From Supervised Learning to Reinforcement Learning Through AlphaZero
Rather than learning from labelled data, our algorithm learns programs using reinforcement learning by interacting with an environment through trial-and-error. Recently, AlphaZero, a reinforcement learning algorithm based on the combined use of neural networks and Monte Carlo Tree Searches (MCTS), has shown incredible results on highly combinatorial problems such as Go, Shogi and Chess. Thus, to enable our algorithm to learn only by interaction with the environment, we extend the original NPI architecture to implement an actor-critic network and propose a variation of AlphaZero to support hierarchies and recursion. We call the resulting algorithm AlphaNPI, as it incorporates both the strength of NPI and AlphaZero. On the one hand, AlphaZero is used as a powerful way to generate data to train the NPI network. On the other hand, we use NPI to bring structure into AlphaZero tree search, allowing it to learn hierarchically programs that can be recursive. This results in a powerful reinforcement learning agent that can learn, with sparse rewards signals, to solve hierarchically complex tasks.
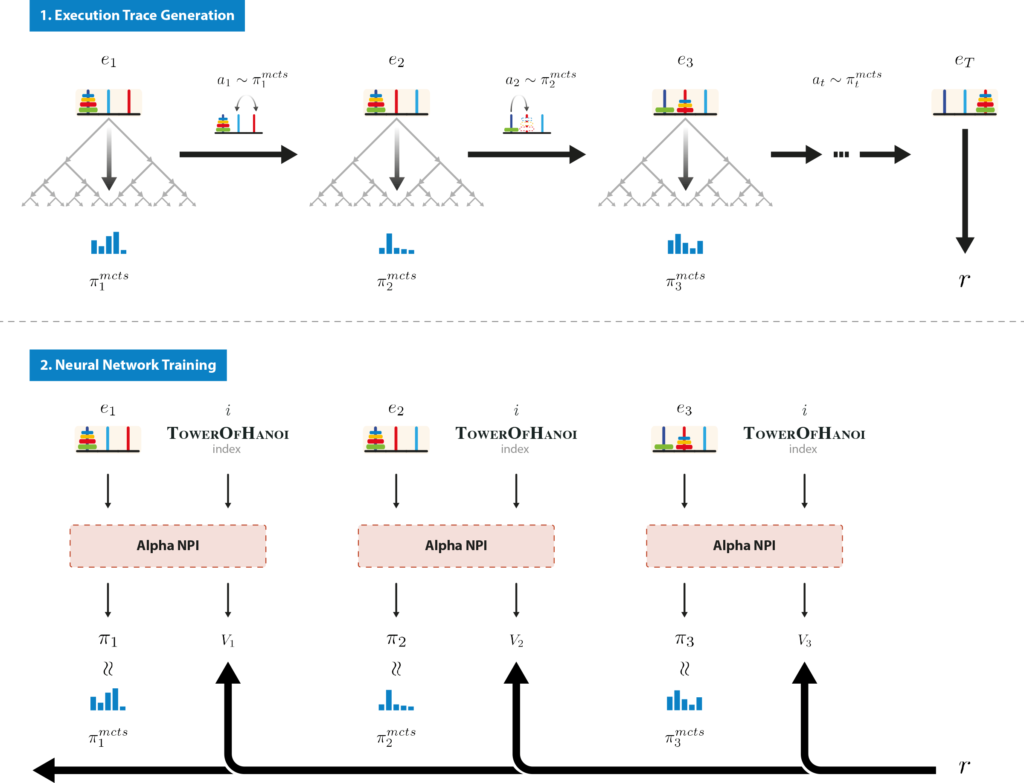
In our environment, the user defines a library of programs and possibly a hierarchy indicating which programs can be called by another. The user also defines correct execution tests for each program, that assesses whether or not the program has been executed correctly. We formulate learning a library of programs as a multi-task reinforcement learning problem, i.e. each task corresponds with learning one of the programs. The associated sparse reward signal is then defined as: 1 if the program terminates in a state verifying its execution condition and 0 otherwise. The agent starts to learn the simplest programs with a set of initially available actions called atomic programs and learns progressively to use them to execute new programs. When a new program has been learnt, it becomes available to the agent as a new action just like the atomic actions. To teach the whole library, we use curriculum learning where the agent starts by learning simple programs first, before learning more complex ones.
AlphaNPI
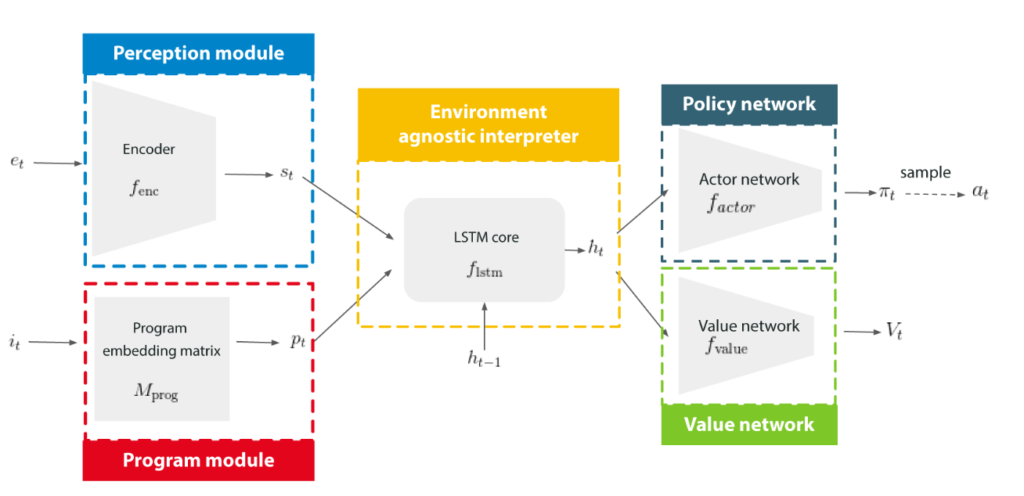
While AlphaNPI extends the original NPI architecture, it keeps its flexibility, simplicity and modularity through its five distinct modules. A perception module encodes the observations from the environment. A program module contains the program embedding matrix where each row corresponds to the embedding of one program of the library. A universal long short-term memory (LSTM) core interprets and executes programs while conditioning on the encoded observations, program embeddings and its internal memory state. A policy network converts the LSTM output to a vector of probabilities over the action space, while a value network uses this output to estimate the value function, which can be interpreted as the degree of confidence that the program will execute correctly.
To execute a program, i.e. to find a correct sequence of programs to call, we use a guided tree search as in AlphaZero. The NPI network is used to estimate priors and values for each node. The main feature of our novel algorithm is its ability to recursively build a new tree to execute a non-atomic program as if it were an atomic-action from the main tree point of view. During the search, if an atomic action is selected, it is directly applied to the environment as in standard AlphaZero. Otherwise, if the selected action is non-atomic, we recursively build a new tree to find how to execute it. As we rely on curriculum learning, we assume that this program has already been learned by the agent, therefore only a small budget of simulations in the subtree is required to execute it. When the subtree search starts, the reward signal adapts to the subprogram to execute. The LSTM internal state is reset to zero. When the subtree search ends, the reward signal takes its previous form and the LSTM internal state gets its previous value. In the main tree, the action has been applied as if it were atomic.
Learning To Bubble Sort
To show that our approach improves compared to the original NPI work, we demonstrate that we can reproduce the results on the Bubble sort algorithm without supervised learning. In this setting, the environment represents a list of \(n\) digits. The atomic actions consist of moving incrementally pointers and swapping elements by sorting the list using only the primary programs requires to find sequences of up to \(5n^2\) actions. Finding solutions in a sparse reward setting when the length n increases, is challenging, and therefore, we rely on compositionality. Before learning to sort the list, the agent is taught five easier programs that it will combine to execute the full Bubble sort algorithm. We trained our agent to sort lists of length between 2 and 7, and observed that it can generalise and sort lists of length up to 60.
The Power of Recursion
Another strength of AlphaNPI is its capability to learn recursive programs. To highlight this skill we chose to consider the Tower of Hanoi puzzle. The game is composed of three pillars and n disks of increasing sizes. Each pillar has a role that is either source, auxiliary or target. At the beginning of the game, all the disks are placed on the source pillar in order of decreasing size, with the largest disk on the bottom. The goal is to move all the disks to the target pillar without ever placing a disk on a smaller one. This game is particularly interesting because, apart from being really simple, it has been carefully studied in mathematics. It has been shown that the minimum number of moves to solve the game is \(2^n -1\).
Once again, finding the right sequence of actions when n increases in a sparse reward setting is incredibly ambitious. In our research, to decrease the problem’s combinatorial explosion, we rely on a recursion. We assume that we can solve the game with \(n-1\) disks, i.e. we can move \(n-1\) disks from one pillar to another. If this action is available, a sequence of three actions can solve the game with an arbitrary number of disks. Thus, finding such a short sequence becomes far easier. We trained our agent to solve, using recursion, the game with two disks and observed that it can generalise up to an arbitrary number of disks.
We also trained our agent to learn the recursive version of the Bubble sort algorithm and observed complete generalisation capabilities.
To Plan or Not To Plan
In standard model-free reinforcement learning, a policy network maps directly observations to actions. To solve problems when no model of the world is available, the agent makes observations and directly decides from these which decision to take. However, in most real-life tasks we have good knowledge of a model. When we play the Tower of Hanoi puzzle, we know what the resulting game state will be if we decide to move a disk. Therefore, instead of taking direct actions and observing the result before taking a new action, most of the time we will imagine what the repercussion of an action is before taking it, i.e. we plan. When a model of the world is known or easy to learn, planning seems to improve over direct interaction. We verify this assumption in our work. When the AlphaNPI network has been trained to solve a problem, we can test its generalisation capabilities after the training with or without planning. In other words, to test the agent we can use the neural network alone, or use a tree search guided by the network. We observe that the AlphaNPI agent performs significantly better in post-training conditions when using planning.
Conclusion and Further Work
We proposed a novel deep reinforcement learning agent, AlphaNPI, that harnesses the power of compositionality and recursion to learn complex programs such as solving the Tower of Hanoi puzzle with an arbitrary number of disks, or Bubble sorting lists of digits using simple atomic actions. While our test domains are complex along some axes, e.g. recursive and combinatorial, they are simple compared to others, e.g. when the environment model is available and the actions considered are discrete. A natural next step would be to consider robotics environments. Here, it is important to also learn perception modules and libraries of skills that may rely only on continuous actions, such as applying continuous torques on robot joints to achieve transfer to new tasks. It will be very exciting to assess our algorithm performance in such complex environments.
