(Part 2/4)
In our introduction to meta-reinforcement learning, we presented the main concepts of meta-RL:
- Meta-Environments are associated with a distribution of distinct MDPs called tasks.
- The goal of Meta-RL is to learn to leverage prior experience to adapt quickly to new tasks.
- In Meta-RL, we learn an algorithm during a step called meta-training. At meta-testing, we apply this algorithm to learn a near-optimal policy.
Previous post: A simple introduction to Meta-Reinforcement Learning
In this post, we introduce our first Meta-RL algorithm: MAML (Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks). With MAML, you can train agents that quickly adapt in almost any dense-reward environment. Let’s detail how it works.
Transfer Learning and Multi-Task Learning
From fine-tuning to MAML
The first natural way to learn a new task is to use transfer learning via fine-tuning (e.g. fine-tuning of a ResNet trained on ImageNet). However, these methods still require a large amount of data and are not suitable for fast few-shot adaptation. Moreover, in meta-learning, we have a distribution of meta-training tasks instead of a single task. Therefore, another method might be to do multi-task learning, i.e. train an optimal policy over all these tasks before doing a fine-tuning adaptation. Hence, the policy should optimise the objective

where
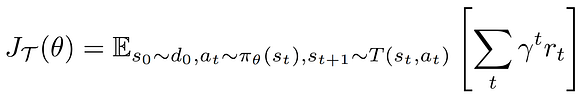
before applying n steps of fine-tuning adaptation:

Again, a major flaw of this method is that the initial parameter θ is optimised to maximise the average return over all tasks but does not guarantee any fast adaptation. Can we find a better initialisation?
This is where MAML [9] comes into play. Can we directly optimise the initialisation parameter to guarantee good adaptation? In MAML, the parameters of the model are explicitly trained to provide a high performance after fine-tuning via gradient descent. Let’s see how we can do that!
MAML Algorithm
Meta-testing goal
Before explaining how to train MAML (meta-training), let’s define what we would expect at meta-test time. Considering that we have found a good initialisation parameter θ from which we can perform efficient one-shot adaptation, and given a new task, the new parameter θ’, obtained by gradient descent, should achieve a good performance on the new task. The figure below illustrates how MAML should work at meta-test time. We are looking for a pretrained parameter that can reach near-optimal parameters for every task in one (or a few) gradient step(s)
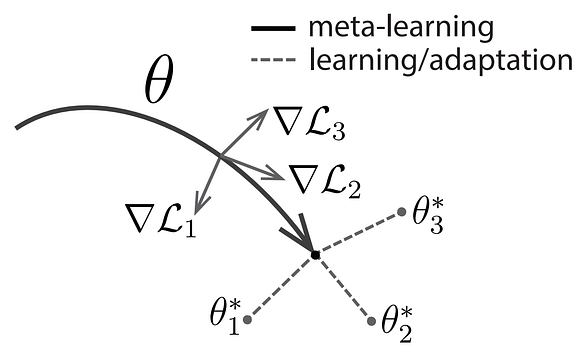

Meta-training
So now, we know what our meta-testing algorithm should look like. Therefore, given a learning rate α for the fine-tuning step, θ should minimise

Optimising this objective is the goal of the meta-training procedure. This objective is differentiable and the gradient is:
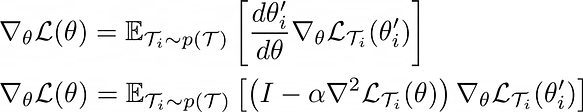
Therefore, we can minimise the objective using policy gradient methods:


This figure illustrates how MAML works during meta-training:

The meta-training algorithm is divided into two parts:
- Firstly, for a given set of tasks, we sample multiple trajectories using θ and update the parameter using one (or multiple) gradient step(s) of the policy gradient objective. This is called the inner loop.
- Second, for the same tasks, we sample multiple trajectories from the updated parameters θ’ and backpropagate to θ the gradient of the policy objective. This is called the outer loop.
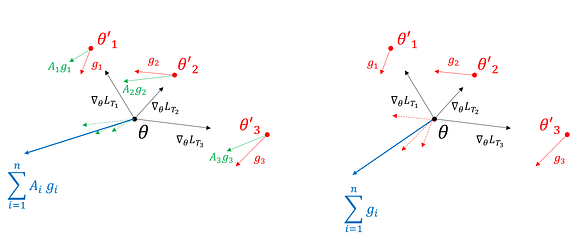
First-order MAML
As illustrated by the previous figure, MAML requires second-order derivatives to compute the gradient at θ. Surprisingly, if we omit the second-order term in matrix A and use the approximation A = I, we also obtain very good results. This algorithm is called first-order MAML (FOMAL). It might be preferable to use it when the dimensions are prohibitively large and the second-order derivatives require too many resources. This figure illustrates how FOMAML differs from MAML:
MAML on MuJoCo
This clip illustrates the behaviour of MAML on the Forward/Backward HalfCheetah environment [9] presented in the previous post. After 1 gradient step, the agent’s policy solves the problem.
A Simple Extension: CAVIA
MAML is a great algorithm, but there is room for improvement. In particular, the need to do a full gradient descent step on all the weights suffers from two major defaults:
- Firstly, updating all the weights requires computing a large gradient demanding a lot of memory and compute.
- Second, the gradient descent updates all the weights based on a few data points only. This is prone to overfitting.
Task-specific and task-independent learning
As mentioned earlier, one goal of meta-learning is to learn the underlying characteristics common to all tasks while recognising task-specific characteristics. Another goal is to quickly identify a task based on little experience and adapt the policy accordingly.
Hence a natural and elegant idea to extend MAML: explicitly separate task-specific and task-independent components in the neural network. The task-independent weights are learned at meta-training. At meta-testing, we simply adapt the task-specific neurons (also called the context) to the new task. With CAVIA [10], we don’t need multiple copies of the neural network because the weights are never modified in the inner loop. We can simply update the context parameters in parallel on multiple tasks in a highly memory-efficient way.
Context adaptation
Here is the general formulation of CAVIA:

Every layer in the network has a set of neurons h that are task-independent and a set of neurons ϕ that are task-specific. These task-specific neurons are initialised at 0 and updated, for a given taskand trajectory, by a gradient ascent step in order to maximise the policy gradient objective:
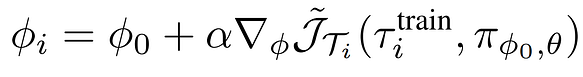
During meta-training, to learn the parameters θ, we use a gradient ascent step on a new trajectory based on the updated context parameters ϕ:
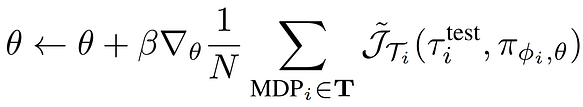
As with MAML, this gradient step requires second-order derivatives to take into account the dependence of ϕ on θ. And, in the same way, we can also do a first-order approximation to neglect the higher-order term.
CAVIA on MuJoCo tasks
In the MuJoCo meta-environments introduced in the previous blog from [9], CAVIA is applied with a 2-layered neural network and takes into account the context only on the input layer.
Here is an illustration of CAVIA on HalfCheetahDir forward/backward:
Conclusion
- The first idea to adapt to a new task is to use fine-tuning from another similar task.
- To find the best initialisation, MAML directly optimises the loss after one gradient step.
- MAML can quickly adapt to new environments and reach near-optimal return.
- MAML uses second-order derivatives during meta-training. It is possible to use a first-order approximation to reduce the computational needs without significantly degrading performance: this is First-Order MAML (FOMAML).
- In order to account for the difference between task-specific and task-independent components of the neural network, we can learn separately the weights and the context of the neural network (CAVIA).
- CAVIA is easier to parallelise, requires less memory and compute, while outperforming MAML on MuJoCo tasks.
References
[1] Adria Puigdomenech Badia, Bilal Piot, Steven Kapturowski, Pablo Sprechmann, Alex Vitvitskyi, Zhaohan Daniel Guo, and Charles Blundell. Agent57: Outperforming the atari human benchmark. CoRR, abs/2003.13350, 2020.
[2] Julian Schrittwieser, Ioannis Antonoglou, Thomas Hubert, Karen Simonyan, Laurent Sifre, Simon Schmitt, Arthur Guez, Edward Lockhart, Demis Hassabis, Thore Graepel, Timothy P. Lillicrap, and David Silver. Mastering atari, go, chess and shogi by planning with a learned model. CoRR, abs/1911.08265, 2019.
[3] Oriol Vinyals and Igor Babuschkin. Grandmaster level in starcraft ii using multi-agent reinforcement learning. 2019.
[4] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin A. Riedmiller. Playing atari with deep reinforcement learning. CoRR, abs/1312.5602, 2013.
[5] Volodymyr Mnih, Adri`a Puigdom`enech Badia, Mehdi Mirza, Alex Graves, Timothy P. Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu. Asynchronous methods for deep reinforcement learning. CoRR, abs/1602.01783, 2016.
[6] John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. Proximal policy optimization algorithms. CoRR, abs/1707.06347, 2017.
[7] Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. CoRR, abs/1801.01290, 2018.
[8] Lasse Espeholt, Hubert Soyer, Remi Munos, Karen Simonyan, Volodymyr Mnih, Tom Ward, Yotam Doron, Vlad Firoiu, Tim Harley, Iain Dunning, Shane Legg, and Koray Kavukcuoglu. IMPALA: scalable distributed deep-rl with importance weighted actor-learner architectures. CoRR, abs/1802.01561, 2018.
[9] Chelsea Finn, Pieter Abbeel, and Sergey Levine. Model-agnostic meta-learning for fast adaptation of deep networks. CoRR, abs/1703.03400, 2017.
10] Abhishek Gupta, Russell Mendonca, Yuxuan Liu, Pieter Abbeel, and Sergey Levine. Meta-reinforcement learning of structured exploration strategies. CoRR, abs/1802.07245, 2018.
[11] Pierre-Alexandre Kamienny, Matteo Pirotta, Alessandro Lazaric, Thibault Lavril, Nicolas Usunier, and Ludovic Denoyer. Learning adaptive exploration strategies in dynamic environments through informed policy regularization. CoRR, abs/2005.02934, 2020.
[12] Emanuel Todorov, Tom Erez, and Yuval Tassa. Mujoco: A physics engine for model-based control. In 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, pages 5026–5033, 2012.
[13] Yan Duan, John Schulman, Xi Chen, Peter L. Bartlett, Ilya Sutskever, and Pieter Abbeel. Rl2: Fast reinforcement learning via slow reinforcement learning, 2016.
[14] Erin Grant, Chelsea Finn, Sergey Levine, Trevor Darrell, and Thomas L. Griffiths. Recasting gradient-based meta-learning as hierarchical bayes. CoRR, abs/1801.08930, 2018.
[15] Alex Nichol, Joshua Achiam, and John Schulman. On first-order meta-learning algorithms. CoRR, abs/1803.02999, 2018.
[16] Luisa M. Zintgraf, Kyriacos Shiarlis, Vitaly Kurin, Katja Hofmann, and Shimon Whiteson. CAML: fast context adaptation via meta-learning. CoRR, abs/1810.03642, 2018.
[17] Kate Rakelly, Aurick Zhou, Deirdre Quillen, Chelsea Finn, and Sergey Levine. Efficient off-policy meta-reinforcement learning via probabilistic context variables. CoRR, abs/1903.08254, 2019.
[18] Jan Humplik, Alexandre Galashov, Leonard Hasenclever, Pedro A. Ortega, Yee Whye Teh, and Nicolas Heess. Meta reinforcement learning as task inference. CoRR, abs/1905.06424, 2019.
[19] Luisa M. Zintgraf, Kyriacos Shiarlis, Maximilian Igl, Sebastian Schulze, Yarin Gal, Katja Hofmann, and Shimon Whiteson. Varibad: A very good method for bayes-adaptive deep RL via meta-learning. CoRR, abs/1910.08348, 2019.
[20] Evan Zheran Liu, Aditi Raghunathan, Percy Liang, and Chelsea Finn. Explore then execute: Adapting without rewards via factorized meta reinforcement learning. CoRR, abs/2008.02790, 2020.
Thanks to Ian Davies and Clément Bonnet.


