InstaDeep is delighted to announce that a collaborative research project with a team from the University of Oxford on “Autoregressive neural-network wavefunctions for ab initio quantum chemistry” has been published in Nature Machine Intelligence magazine.
The paper was authored by Dr Thomas Barrett of InstaDeep as well as Prof A. I. Lvovsky and Aleksei Malyshev from the Department of Physics at the University of Oxford. It applies machine learning to the canonical challenge of modelling complex quantum systems, and is InstaDeep’s first foray into the growing intersection of AI and quantum computation. The work also marks the beginning of a wider research initiative within InstaDeep, with the formation of an in-house Quantum Machine Learning team (QML) recently announced.
A grand challenge: solving the many-body Schrödinger equation
Newton’s famous laws were pioneered in the 17th century and still provide a remarkably accurate description of the world humans experience every day. Given sufficient knowledge of a system, it allows scientists to build a model and predict how it will evolve. However, during the early 20th century it became clear that so-called Newtonian (classical) mechanics was not sufficient to deal with speeds and scales far beyond those for which it was created. This led to Einstein’s theories of special and general relativity — that can work with systems approaching the fundamental limit of the speed of light — and quantum mechanics — which describes nature at atomic and subatomic scales. The quantum world is inherently probabilistic and here many intuitions break down. Famous examples include Schrödinger’s thought-experiment where his eponymous cat is simultaneously both dead and alive, and wave-like particles that do not have a defined position but are instead smeared out across space with some probability distribution.
Despite these weird properties, quantum mechanics is fundamental to modern science and technology. Schrödinger’s equation lies at the very heart of quantum mechanics and can be thought of as a quantum analog to Newton’s laws. It relates the state of a quantum system to its energy and allows science to understand how it will behave in nature. For molecules, this means that solving the many-body Schrödinger equation describing the interactions of heavy nuclei and orbiting electrons can, in principle, provide full access to chemical properties such as the system’s energy, stability, or possible reactions it may undergo.
However, whilst utilising fundamental theories to model chemistry and molecules from first principles is an alluring prospect, in practice the remarkable complexity of these systems means that all but the simplest of cases are intractable to solve analytically. Decades of research has developed an array of numerical methods for so-called ”ab initio” quantum chemistry, and recent years have seen this problem class marked-out as one of the most promising applications of quantum computing. However, with numerical methods ultimately forced to trade-off accuracy for computational feasibility, and quantum computers still in their nascent stages, solving the many-body Schrödinger equation in quantum chemistry remains an outstanding challenge.
A primer: quantum chemistry and neural network quantum states
In quantum chemistry, electrons are considered to exist within molecular orbitals – mathematical functions that describe the probability of finding an electron in a specific region of space around the molecule. To model the system, a basis set of orbitals is considered,and a probability amplitude assigned to every possible configuration which the electrons could fill. The wavefunction is a function that takes as its input a specific configuration and returns a probability amplitude that relates to how likely it is that the electrons are in this state. In its most fundamental form, the task of solving a molecular Schrödinger equation is to find the wavefunction with lowest energy (the “ground state” in which the molecule could be expected to be found in nature). However, the number of ways in which electrons can fill the orbitals is enormous, therefore explicitly enumerating and optimising the amplitude of every possible electronic configuration is intractable for medium- to large-scale molecules.
A leading approach to deal with this intractable scaling is to propose a parameterised function (an “ansatz”) that maps configurations to probabilities, and directly optimise the free parameters to modify the wavefunction they implicitly encode. It is not practical to calculate the full wavefunction (i.e. every configuration’s probability) so it is instead approximated by sampling many electronic configurations from the encoded probability distribution. This optimises the wavefunction towards lower energy states using what are known as Variational Monte Carlo (VMC) methods.
The solution quality provided is heavily dependent on the expressiveness of the ansatz and the ease with which it can be optimised. An ansatz implemented on a quantum computer is a promising early application of quantum machine learning, however traditional machine learning also provides a powerful toolkit for working in high-dimensional spaces. This motivated the development of neural-network quantum states (NNQS) which represent the wavefunction with a neural network. Whilst initially developed for applications in condensed matter physics, NNQS provides a powerful and flexible ansatz that is not constrained by the simplifying assumptions of other traditional approximations.

A bespoke neural network wavefunction for quantum chemistry
The primary innovation is the demonstration of an NNQS specifically tailored towards learning molecular wavefunctions. Prior work has mostly focussed on a class of models called Restricted Boltzmann Machines (RBMs), which are powerful but have major drawbacks. Firstly, RBMs use an expensive sampling procedure to generate electron configurations from the underlying wavefunction, limiting the scalability of these models. Additionally, RBMs are “black-box” models that do not reflect significant prior knowledge of the form physically viable wavefunctions can take. The authors instead focused on a so-called autoregressive models, where rather than modelling the probability of a given configuration of all the electrons in a single step, the model is decomposed into a series of conditional distributions which ask “what is the probability distribution over of the i-th electron(s) state, given we know the state of electrons 1 to i-1?”. Their neural autoregressive quantum state (NAQS) has two major advantages.
- The model can be exactly sampled using a highly efficient and parallelisable procedure. In practice, at each optimisation step up to $10^{12}$ samples were used (an arbitrarily chosen upper limit), which is 6 orders of magnitude beyond what the nearest prior works with RBMs could manage.
- Known physical priors (such as conservation of the total number of electrons and other quantum mechanical properties) can be embedded into the network architecture.
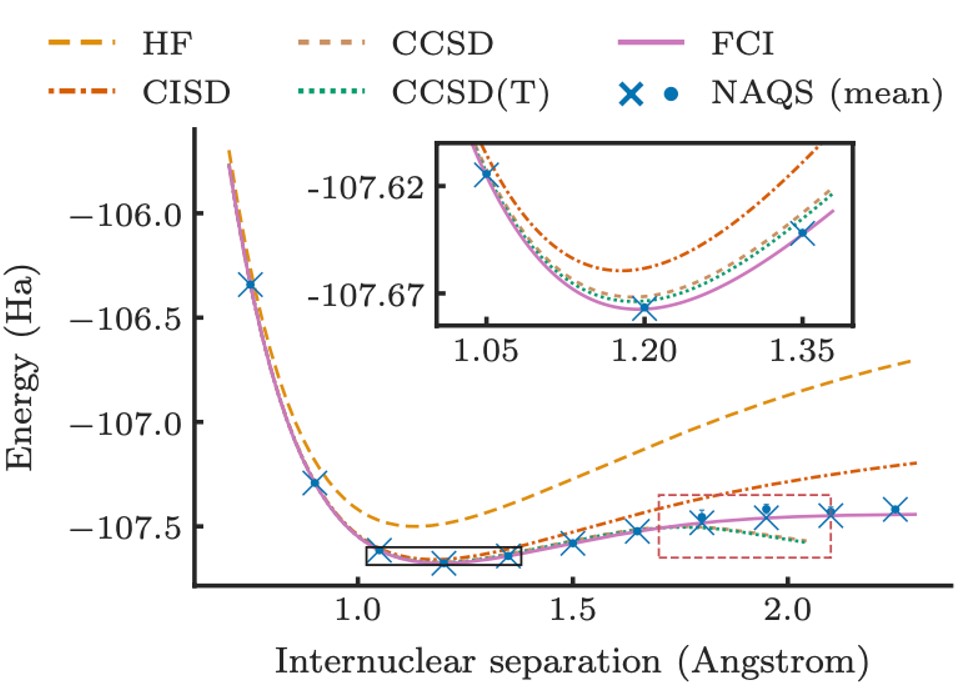
Ultimately, this realised better accuracy and scale to molecules at up to 25 times larger than what was previously possible using NNQS in this problem setting. Beyond empirical performance, the work represents one of the most ambitious applications of NNQS to date, and further highlights the growing role of ML in tackling nature’s most intractable challenges.
About Nature Machine Intelligence
Nature Machine Intelligence publishes high-quality original research and reviews in a wide range of topics in machine learning, robotics and AI. We also explore and discuss the significant impact that these fields are beginning to have on other scientific disciplines as well as many aspects of society and industry. There are countless opportunities where machine intelligence can augment human capabilities and knowledge in fields such as scientific discovery, healthcare, medical diagnostics and safe and sustainable cities, transport and agriculture. At the same time, many important questions on ethical, social and legal issues arise, especially given the fast pace of developments. Nature Machine Intelligence provides a platform to discuss these wide implications — encouraging a cross-disciplinary dialogue — with Comments, News Features, News & Views articles and also Correspondence.
Like all Nature-branded journals, Nature Machine Intelligence is run by a team of professional editors and dedicated to a fair and rigorous peer-review process, high standards of copy-editing and production, swift publication, and editorial independence.

